数据结构:练习题二
练习题二
一、
1.
2.
3.
4.
5.
6.
7.
8.
9.
10.
二、
1.设指针变量front
(A)
front->next=s
(C)
rear->next=s
2.执行一趟快速排序能够得到的序列是( )。
(A)
[41
(B)
[45
(C)
[63
(D)
[12
3.设一条单链表的头指针变量为head
(A) head==0 (B) head->next==0
(C) head->next==head (D)
head!=0
4.时间复杂度不受数据初始状态影响而恒为O(nlog2n)
(A)
5.设二叉树的先序遍历序列和后序遍历序列正好相反,则该二叉树满足的条件是( )。
(A)
(C)
6.一趟排序结束后不一定能够选出一个元素放在其最终位置上的是( )。
(A)
7.设某棵三叉树中有40
(A)
3
(B) 4 (C) 5 (D) 6
8.顺序查找不论在顺序线性表中还是在链式线性表中的时间复杂度为( )。
(A)
O(n)
(B) O(n2) (C) O(n3) (D) O(1og2n)
9.二路归并排序的时间复杂度为( )。
(A)
O(n)
(B) O(n2) (C)
O(nlog2n) (D) O(1og2n)
10.设有序表中的元素为(13
(A)
1
(B) 2 (C) 3 (D) 4
三、
1.
func( )
{ initstack(s);
scanf(“%d”,&n);
while(n)
{ push(s, n%8); n=n/8; }
while(!Emptystack (s))
{ pop(s,x); printf(“%d”,x); }
}
2.
(1)计算出每一个元素的散列地址并在下图中填写出散列表:
0 1 2 3 4 5 6
|
|
|
|
|
|
|
|
3.
(1)
(2)
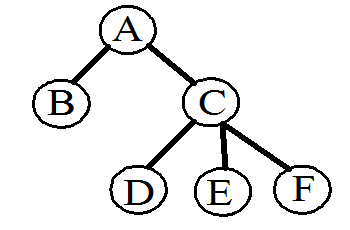
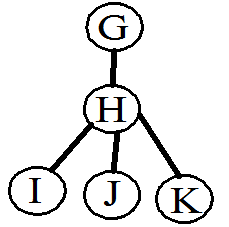
(a) (b)
4.
5.
E={(1,2)3,(1,3)5,(1,4)8,(2,5)10,(2,3)6,(3,4)15,
(3,5)12,(3,6)9,(4,6)4,(4,7)20,(5,6)18,(6,7)25};
用克鲁斯卡尔算法得到最小生成树,试写出在最小生成树中依次得到的各条边。
四、 算法题(每小题10分,共20分)
1.
bool Find(BTreeNode*
BST,ElemType& item)
{
if (
return (2
else {
if (item==BST->data){
item=BST->data;//
return
else if(item<BST->data)
return Find(
else
return Find( (5
}
}
2
其中结点的存储结构如下图所示:
|
data |
next |
|
|
|
结点的结构类型定义如下:
typedef char datatype;
typedef struct node
{
datatype data;
struct node *next;
}lklist;
void split(lklist *head,lklist
*&ha,lklist *&hb,lklist *&hc)
{
}


