图的应用：最小生成树P165

名词介绍：

连通图：在无向图中，若任意两个顶点vi与vj都有路径相通，则称该无向图为连通图。
强连通图：在有向图中，若任意两个顶点vi与vj都有路径相通，则称该有向图为强连通图。
连通网：在连通图中，若图的边具有一定的意义，每一条边都对应着一个数，称为权；权代表着连接连个顶点的代价，称这种连通图叫做连通网。
生成树：一个连通图的生成树是指一个连通子图，它含有图中全部n个顶点，但只有足以构成一棵树的n-1条边。一颗有n个顶点的生成树有且仅有n-1条边，如果生成树中再添加一条边，则必定成环。
最小生成树：在连通网的所有生成树中，所有边的代价和最小的生成树，称为最小生成树。

构造最小生成树

1、普利姆算法Prim （加点法）

假设N=(V,{E})是连通网，TE为最小生成树的边集合。
（1）初始U={u0}(u0∈V),TE=φ；
（2）在所有u∈U, v∈V-U的边(u,v)中选择一条代价最小的边（u0，v0）并入集合TE，同时将v0并入U；（并修正U-V中各顶点到U的最短边信息）
（3）重复步骤（2），直到U=V为止。
此时，TE中含有n-1条边，T=（V，{TE}）为N的最小生成树。
普里姆算法是逐步向U中增加顶点的“加点法”。 

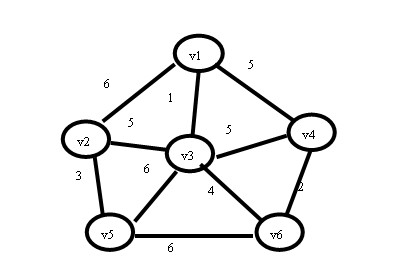
例如用普利姆算法画出下图的最小生成树 

练习：设无向图G（如图所示），给出该图的最小生成树上边的集合并计算最小生成树各边上的权值之和。

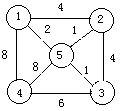
答案：E={(1,5),(5,2),(5,3),(3,4)},W=10   

2、克鲁斯卡尔Kruskal （加边法）

（1）将n个顶点构成n个集合；
（2）按权值由小到大的顺序选择边，选择两个邻接顶点不在同一顶点集合内的边，将该边放入生成树的边集合中。同时将该边关联的两个顶点所在的顶点集合合并；
（3）重复(2)，直到所有顶点均在同一顶点集合内。
克鲁斯卡尔算法逐步增加生成树所包含的边–“加边法”。