哈夫曼树介绍
哈夫曼树(Huffman Tree)是最优二叉树。给定n个权值作为n个叶子的结点,构造一棵二叉树,若树的带权路径长度达到最小,这棵树则被称为哈夫曼树。哈夫曼树是带权路径长度最短的树,权值较大的结点离根较近。
名词介绍
1、路径和路径长度
在一棵树中,从一个结点往下可以达到的孩子或孙子结点之间的通路,称为路径。通路中分支的数目称为路径长度。若规定根结点的层数为1,则从根结点到第L层结点的路径长度为L-1。
2、结点的权及带权路径长度
若将树中结点赋给一个有着某种含义的数值,则这个数值称为该结点的权。结点的带权路径长度为:从根结点到该结点之间的路径长度与该结点的权的乘积。
3、树的带权路径长度
树的带权路径长度规定为所有叶子结点的带权路径长度之和,记为WPL。
哈夫曼树构建步骤:
1、根据给定的n个权值,构造n棵只有根结点的二叉树,构成一个森林F;
2、在森林F中选取权值最小的两个树作为左右子树,构造一棵新的二叉树,且根节点的权值为左右子树根结点的权值之和;
3、在森林F中删除选取的那两棵树,同时将新的二叉树放入森林中;
4、重复2和3,直到F只含一棵树为止。
哈夫曼树构造经验总结:
1、为了使得到的哈夫曼树的结构尽量唯一,通常规定生成的哈夫曼树中每个结点的左子树根结点的权小于等于右子树根结点的权。
2、每次将森林中最小的两棵树组成新的(不是每次都以新的为主)。
3、哈夫曼树并不唯一。
哈夫曼编码Huffman 实例
P147假设用于通信的电文仅由8个字母组成,字母在电文中出现的频率分别为0.07, 0.19, 0.02, 0.06, 0.32, 0.03, 0.21, 0.10。
1)试为这8个字母设计哈夫曼编码。
2)设计另一种有二叉树表示的登场编码方案。
3)对于上述实例,比较两种方案的优缺点。
画图,构造哈夫曼树
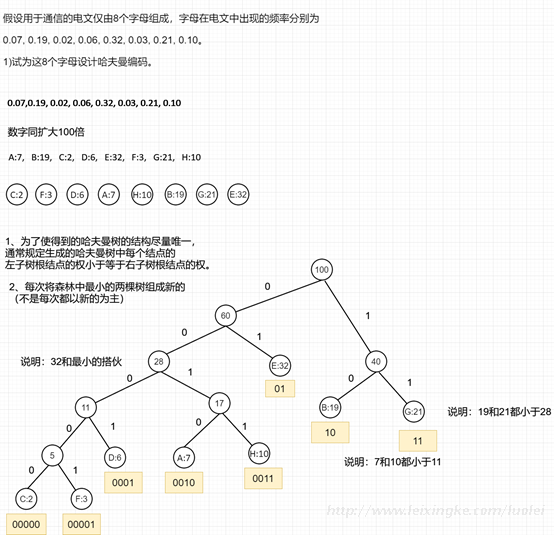
1)试为这8个字母设计哈夫曼编码。
方案一:
|
字母 |
对应编码 |
频率 |
|
A |
0010 |
0.07 |
|
B |
10 |
0.19 |
|
C |
00000 |
0.02 |
|
D |
0001 |
0.06 |
|
E |
01 |
0.32 |
|
F |
00001 |
0.03 |
|
G |
11 |
0.21 |
|
H |
0011 |
0.10 |
2)方案二:使用0~7的二进制表示形式是另一种编码方案。
|
字母 |
对应编码 |
频率 |
|
A |
000 |
0.07 |
|
B |
001 |
0.19 |
|
C |
010 |
0.02 |
|
D |
011 |
0.06 |
|
E |
100 |
0.32 |
|
F |
101 |
0.03 |
|
G |
110 |
0.21 |
|
H |
111 |
0.10 |
3)对于上述实例,比较两种方案的优缺点。
方案1的WPL=2(0.19+0.32+0.21)+4(0.07+0.06+0.10)+5(0.02+0.03) =2.61
方案2的WPL=3(0.19+0.32+0.21+0.07+0.06+0.10+0.02+0.03)=3
结论:哈夫曼编码优于等长二进制编码。即方案一优于方案二。


